
난이도
입문(Lv. 0)
문제
문제 설명
첫 번째 분수의 분자와 분모를 뜻하는 numer1, denom1, 두 번째 분수의 분자와 분모를 뜻하는 numer2, denom2가 매개변수로 주어집니다. 두 분수를 더한 값을 기약 분수로 나타냈을 때 분자와 분모를 순서대로 담은 배열을 return 하도록 solution 함수를 완성해보세요.
제한사항
- 0 <numer1, denom1, numer2, denom2 < 1,000
입출력 예

제출 답안
// Playhground에서는 잘 작동하지만 프로그래머스에서는 오류가 발생했던 코드
func solution(_ numer1:Int, _ denom1:Int, _ numer2:Int, _ denom2:Int) -> [Int] {
var numer3: Int, denom3: Int = 0
if denom1 == denom2 {
numer3 = numer1 + numer2
denom3 = denom1
} else {
numer3 = (numer1 * denom2) + (numer2 * denom1)
denom3 = denom1 * denom2
}
let gcd = gcd(numer3, denom3)
numer3 /= gcd
denom3 /= gcd
return [numer3, denom3]
}
func gcd(_ a: Int, _ b: Int) -> Int {
if b == 0 {
return a
} else {
return gcd(b, a % b)
}
}

gcd 함수를 맨 위로도 올려보고, solution 함수 내부의 중첩함수로 넣어봐도...
오류가 해결되지 않았다 ㅠㅠ...
무슨 문제일지 구글링을 돌려보다가 스오플에서 발견한... 변수가 이미 사용되고 있을 수 있다는 해결방법!
설마...
에이 ㅎ 설마
gcd 변수 이름을 임의로 gcd1로 변경해 보았다...

변수 선언 시 네이밍에 신경써야 하는 이유를 이렇게 하나 또 알아간다...

최종 제출 답안
// gcd 변수를 greatestCommonDivison으로 네이밍만 변경
import Foundation
func solution(_ numer1:Int, _ denom1:Int, _ numer2:Int, _ denom2:Int) -> [Int] {
var numer3: Int, denom3: Int = 0
if denom1 == denom2 {
numer3 = numer1 + numer2
denom3 = denom1
} else {
numer3 = (numer1 * denom2) + (numer2 * denom1)
denom3 = denom1 * denom2
}
let greatestCommonDivison = gcd(numer3, denom3)
numer3 /= greatestCommonDivison
denom3 /= greatestCommonDivison
return [numer3, denom3]
}
func gcd(_ a: Int, _ b: Int) -> Int {
if b == 0 {
return a
} else {
return gcd(b, a % b)
}
}
다른 Solution 분석 및 학습
// 고차함수 filter를 이용한 풀이
func solution(_ denum1:Int, _ num1:Int, _ denum2:Int, _ num2:Int) -> [Int] {
let x = denum1 * num2 + denum2 * num1
let y = num1 * num2
let xList = (1...x).filter{x % $0 == 0}
let yList = (1...y).filter{y % $0 == 0}
let maxNum = xList.filter{yList.contains($0)}.max()! ?? 1
return [x / maxNum, y / maxNum]
}
풀이들을 보면 분모를 서로 곱하는 방법을 가장 많이 사용했는데,
나의 경우 분모가 같을 때는 분자를 서로 곱하는 과정을 안 해도 되지 않을까? 하는 생각에
if 조건문으로 분모가 같은 경우에는 곱하기 연산을 수행하지 않고 바로 더하도록 했다.
문제 풀이를 보다보니 filter를 이용한 풀이가 있었는데 이의 경우에도 분모를 서로 곱한 후 진행하고 있다.
filter 함수와 최대공약수를 구하는 재귀함수 중에 어떤 게 더 풀이가 빠른지는 좀 더 찾아봐야겠다!
기약분수, 최대공약수, 유클리드 호제법
값을 단순히 분자, 분모 형태로 나타내는 것이 아닌 기약 분수로 표현해야 하기에 최대공약수를 구해서 분자, 분모에 각각 나눠줘야 했다!
기약분수를 구하기 위해서는 최대공약수를 알아야 했고, 최대공약수를 구하는 가장 쉬운 방법은 유클리드 호제법이었던 것!
기약분수부터 최대공약수, 유클리드 호제법까지 천천히 알아보도록 하자!
기약분수?
기약분수란?
분자와 분모의 공약수 (Greatest Common Factor, 줄여서 GCF)가 1뿐이어서 더이상 약분되지 않는 분수
유클리드 호제법
유클리드 호제법은 A를 B로 나눈 몫을 Q라 하고, 나머지를 R이라 했을 때,
A,B의 최대공약수는 B,R의 최대공약수와 같다는 정수론!
그림으로 간단히 정리하면...!

이를 이용하면 최대공약수를 쉽게! 구할 수 있다!
최대공약수 알고리즘
유클리드 호제법을 활용한 최대공약수 알고리즘은 아래와 같다!
func gcd(_ a: Int, _ b: Int) -> Int {
print(#function, a, b)
if b == 0 {
return a
} else {
return gcd(b, a % b)
}
}
사실 코드만 딱 띄워두면 잘 모르겠어서 글 설명 추가!
보기 좋은 게 이해하기도 좋잖아요~!
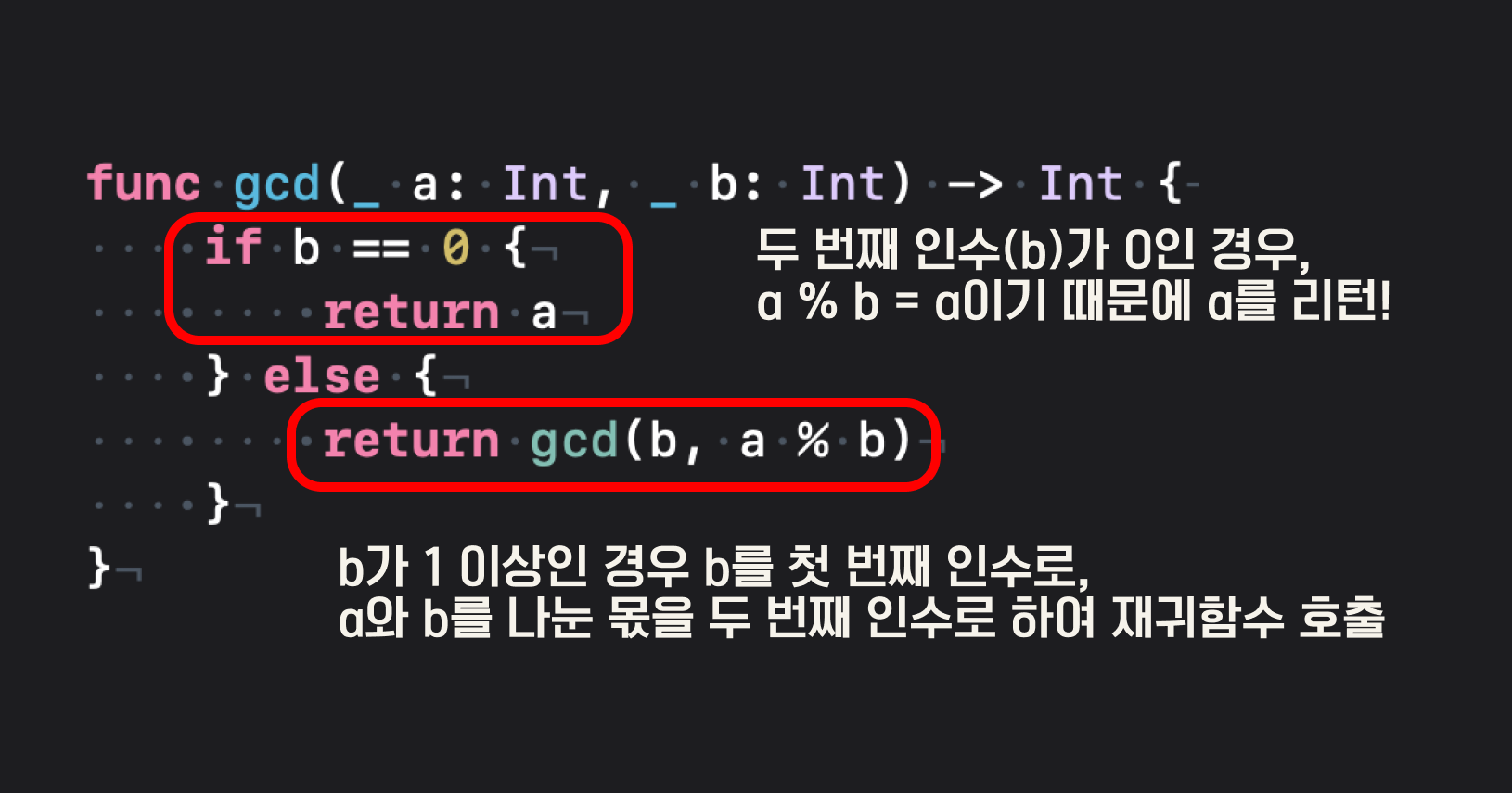
만약 이 함수를 실행시킨다면?
머리로만 계산하기에는 아직 Swift 응애이기 때무넹...
이것 또한 이미지를 활용해서 천천히 알아보는 걸루...!

유클리드 호제법에 재귀함수를 활용하여 최대공약수를 쉽게 구할 수 있었다!
최대공약수를 구하면 두 수의 최소공배수를 구하는 것은 쉽다!
a * b = 최대공약수 * 최소공배수
최소공배수를 구하는 알고리즘은 왠지 문제를 풀다보면 등장할 것 같으니 그때 함께 정리하는 걸로!
삽질로그에 가까웠던 프로그래머스 분수의 덧셈 문제풀이 끝~!!
'Swift > Algorithm' 카테고리의 다른 글
| Swift 프로그래머스 [120810, 1, 2] 나머지 구하기, 중앙값 구하기, 최빈값 구하기 (0) | 2024.02.29 |
|---|---|
| Swift 프로그래머스 [120809] 배열 두 배 만들기, 고차함수 map, return 생략하기! (0) | 2024.02.28 |
| Swift 프로그래머스 [120807] 숫자 비교하기 알고리즘 (0) | 2024.02.09 |
| Swift 프로그래머스 [120806] 두 수의 나눗셈 알고리즘 (0) | 2024.02.08 |
| Swift 프로그래머스 [120805] 몫 구하기 (0) | 2024.02.06 |
